纳维斯托克斯方程,源自19世纪的重要科学成就,至今依然是物理学和工程学中最具挑战性的话题之一。这组方程不仅是流体力学的核心,更是理解和预测自然界中无数现象的关键。从天气变化到航空航天工程,纳维斯托克斯方程的应用广泛而深远。
一、纳维斯托克斯方程的基本理解
纳维斯托克斯方程描述了粘性流体—即实际流体如水和空气—在运动时的速度、压力、密度和体积力之间的关系。它们由法国工程师克劳德-路易-纳维和英国数学家乔治-加布里埃尔-斯托克斯于19世纪分别独立提出。这些方程在数学上表现为一组非线性偏微分方程,解决它们需要高度的数学和物理知识。
纳维斯托克斯方程可以具体分为两类:描述不可压缩流体和可压缩流体的运动。不可压缩流体的方程简化了一些,因为它们假设流体的密度是恒定的;而可压缩流体的方程则必须考虑密度的变化,这使得问题更加复杂。
二、方程的数学表述和物理意义
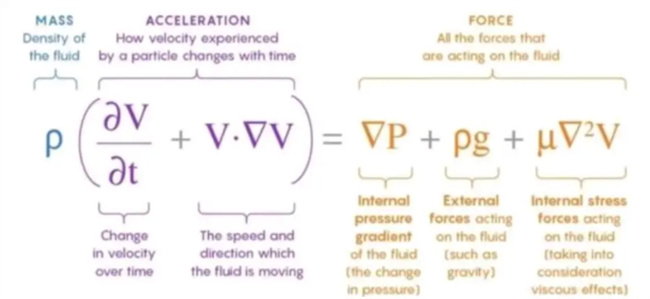
从物理角度来看,纳维斯托克斯方程的一般形式包括动量守恒和质量守恒的方程。在直角坐标系中,动量守恒方程可以表达为流体质点的加速度与作用于流体质点的力之间的平衡。这些力包括压力梯度力、体积力(如重力)、以及由流体粘性引起的内部摩擦力。
数学上,这些方程涉及到速度矢量和压力标量的空间及时间导数,同时还有涉及到流体密度和粘性系数等参数。在具体情况下,根据流体的性质和问题的特定需求,这些方程可能会有所简化。

三、解的存在性和光滑性问题
纳维斯托克斯方程最具挑战性的方面之一是其解的存在性和光滑性问题。简单来说,科学家们至今尚未确定在所有可能的物理条件下,这些方程是否总是有解,以及这些解在数学上是否表现为连续和无奇点。这一问题是著名的“千禧年大奖问题”之一,至今仍未有定论。

四、实际应用和计算挑战
在实际应用中,由于纳维斯托克斯方程的复杂性,除了一些特别简单的情况外,很难获得精确解。因此,工程师和物理学家通常依赖数值方法来近似求解这些方程。这些数值方法,如有限元分析和计算流体动力学(CFD),使我们能够模拟复杂的流体动力行为,从而设计更安全的飞机、更有效的水轮机和更准确的天气预报模型。
纳维斯托克斯方程不仅是流体力学的一个分支,它是连接数学理论、物理实验和工程实践的桥梁。虽然这些方程极具挑战性,但它们在科学和工程的多个领域中扮演着不可或缺的角色。通过深入研究和应用这些方程,我们可以更好地理解和利用那些影响我们日常生活和工业应用的复杂流体现象。






